Zeitwert des Geldes – Erklärung & Berechnung
Autor: Maik Engelkamp
Inhaltlich geprüft von: Philipp Berger
Der Zeitwert des Geldes (englisch: „Time Value of Money“) beschreibt das Prinzip, dass ein bestimmter Geldbetrag heute mehr wert ist als in der Zukunft. Dies liegt daran, dass Geld investiert werden kann und durch Zinsen, Renditen oder andere Erträge im Laufe der Zeit wächst. Zusätzlich spielen Inflation und Risiko eine Rolle, da der reale Wert des Geldes im Laufe der Zeit sinken kann.
🔴 Live-Webinar am 28.04.2025 um 18:30 Uhr
Ausbildung für Vermögensaufbau mit zusätzlichen monatlichen Einnahmen
Lerne, wie du an der Börse ein regelmäßiges Zusatzeinkommen aufbaust. Unterscheide gute von schlechten Aktien, führe eigenständig eine Bewertung durch und erkenne den richtigen Aktienkurs. Lerne außerdem, wie du mit dem Optionshandel einen zusätzlichen Cashflow generierst.
Gute von schlechten Aktien unterscheiden
Profitable Aktien- und Optionsstrategien
In jeder Marktlage Geld verdienen
Plus Gratis-PDF im Webinar: Dein Start in den erfolgreichen Optionshandel
Zeitwert des Geldes – Definition
Der Zeitwert des Geldes ist ein finanzwirtschaftliches Konzept, das besagt, dass jeder Geldbetrag aufgrund seines zwischenzeitlichen Ertragspotenzials (“Opportunitätskosten”) heute einen höheren Wert hat als zu einem zukünftigen Zeitpunkt. Werden die zukünftigen Zahlungsströme einer Investition auf den heutigen Wert abgezinst (sog. “Diskontierung”), spricht man vom Barwert (engl. “Present Value”).
Zeitwert des Geldes – Berechnung
Die grundlegende Formel für den Zukunftswert einer einzelnen Zahlung unter der Annahme, dass Zinsen mehrfach im Jahr kapitalisiert werden (z. B. monatlich oder quartalsweise), ist wie folgt aufgebaut:
Die Variablen sind hierbei wie folgt definiert:
- FV (Future Value) = Zukunftswert des Geldes
- PV (Present Value) = Barwert des Geldes
- i (Interest Rate) = Zinssatz pro Jahr
- n (Number of compounding periods p.a.) = Anzahl der Aufzinsungsperioden pro Jahr, z.B. monatlich n = 12
- t (Time) = Anzahl der Jahre
Diese Formel ist eine Erweiterung der einfachen Zinseszinsformel, die verwendet wird, wenn Zinsen nur einmal im Jahr anfallen:
Bedeutung des Konzepts
Investoren bevorzugen es, Geld sofort zu erhalten, anstatt denselben Betrag erst in der Zukunft zu bekommen. Der Hauptgrund dafür liegt in den Opportunitätskosten – das heute verfügbare Kapital kann investiert werden und durch Zinsen oder Renditen wachsen. Ein klassisches Beispiel ist ein Sparkonto: Dort erwirtschaftet ein angelegter Betrag Zinsen, deren Höhe maßgeblich von der Zinspolitik der Zentralbank beeinflusst wird.
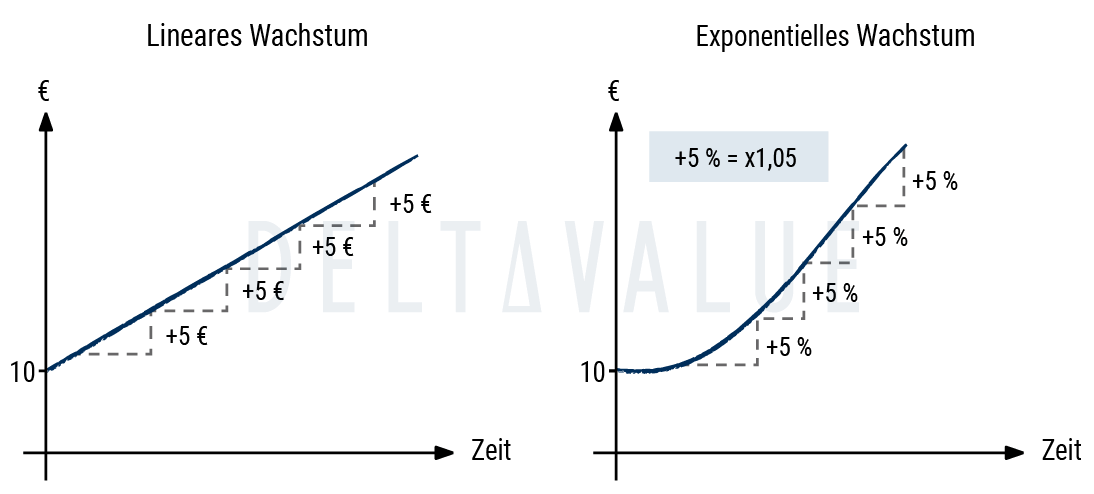
Über die Zeit führt die Wiederanlage von Zinsen dazu, dass nicht nur das ursprüngliche Kapital, sondern auch die bereits erwirtschafteten Zinsen weiter verzinst werden. Dadurch wächst das Kapital immer schneller – ein Effekt, der als Zinseszinseffekt bekannt ist. Selbst bei einem konstanten Zinssatz steigt der absolute Zinsertrag jährlich, da die Berechnungsbasis kontinuierlich wächst.
Andererseits verliert nicht investiertes Kapital mit der Zeit an Wert. Wer beispielsweise 1.000 Euro über drei Jahre unverzinst aufbewahrt, verzichtet auf mögliche Erträge. Zusätzlich reduziert die Inflation die Kaufkraft des Geldes, sodass derselbe Betrag in der Zukunft weniger wert ist. Dies gilt jedoch nur in Zeiten steigender Preise – während einer Deflation kann der Geldwert theoretisch sogar steigen.
Beispiel zur Veranschaulichung des Konzepts
Ein Anleger kann wählen, ob er heute 10.000 Euro oder in zwei Jahren 10.000 Euro erhält. Entscheidet er sich für den sofortigen Erhalt, kann er das Geld investieren – zum Beispiel auf einem Sparkonto mit 5 % jährlichem Zins. Nach zwei Jahren hätte sein Kapital durch den Zinseszinseffekt bereits 11.025 Euro erreicht.
Entscheidet er sich stattdessen für die verzögerte Auszahlung, entgeht ihm dieser Gewinn – die Opportunitätskosten betragen in diesem Fall 1.025 Euro. Trotz des gleichen Nennwerts sind 10.000 Euro heute also real mehr wert als in der Zukunft.
Der Zeitwert des Geldes ist nicht nur eine finanzielle, sondern auch eine psychologische Entscheidung. In seiner Sonderform, der hyperbolischen Diskontierung, bevorzugen Menschen kurzfristige Belohnungen überproportional und entwerten langfristige Vorteile stark. Dadurch handeln sie oft irrational, etwa indem sie zu wenig für die Rente sparen oder teure Kredite aufnehmen.
Opportunitätskosten
Die Opportunitätskosten sind ein zentrales Element des Zeitwerts des Geldes. Geld kann nur wachsen, wenn es investiert wird und eine positive Rendite erzielt. Wird es hingegen nicht angelegt, verliert es an Wert – sei es durch entgangene Zinsen, Renditen oder die Inflation.
Daher ist ein Geldbetrag, der erst in der Zukunft ausgezahlt wird, weniger wert als derselbe Betrag heute, da in der Zwischenzeit Einnahmemöglichkeiten ungenutzt bleiben. Die Differenz zwischen dem heutigen und dem zukünftigen Wert spiegelt die Opportunitätskosten der Verzögerung wider.
Aufzinsungseffekt beim Zeitwert des Geldes
Die Anzahl der Aufzinsungsperioden hat einen dramatischen Einfluss auf die Berechnungen. Dies ist durch den Zinseszinseffekt begründet. Wenn die Anzahl der Aufzinsungsperioden auf vierteljährlich, monatlich oder täglich erhöht wird, ergeben sich folgende Berechnungen für den Barwert (BW) einer einjährigen Investition von 10.000 EUR bei einem Zinssatz von 10%:
- Vierteljährlich: Die Zinsen werden viermal im Jahr berechnet und dem Kapital hinzugefügt, wodurch die Berechnungsgrundlage quartalsweise wächst.
- Monatlich: Die Zinsen werden zwölfmal im Jahr berechnet, wodurch die Berechnungsgrundlage monatlich ansteigt.
- Täglich: Die Zinsen werden 365-mal im Jahr berechnet, sodass sich die Berechnungsgrundlage täglich leicht erhöht.
Der Zeitwert des Geldes hängt also nicht nur vom Zinssatz und vom Zeithorizont ab, sondern auch von der Anzahl der Aufzinsungsperioden (Zinsausschüttungen).
Anwendung im Finanzwesen
Der Zeitwert des Geldes spielt eine zentrale Rolle in nahezu allen Bereichen des Finanzwesens und beeinflusst maßgeblich den Entscheidungsprozess von Investoren, Unternehmen und Finanzinstituten.
Ein Anwendungsgebiet ist die Discounted-Cashflow-Analyse (DCF) – eine der wichtigsten Methoden zur Bewertung von Investitionen, Unternehmen und Projekten. Sie basiert darauf, zukünftige Zahlungsströme auf ihren heutigen Wert abzuzinsen, um fundierte Investitionsentscheidungen zu treffen.
Auch in Finanzplanung und Risikomanagement spielt der Zeitwert des Geldes eine Schlüsselrolle. Beispielsweise kalkulieren Pensionsfondsmanager, wie heutige Einlagen angelegt werden müssen, damit sie über die Jahre genügend Kapital generieren, um den Ruhestandsbedarf der Versicherten zu decken.
Ebenso berücksichtigen Banken und Kreditgeber dieses Prinzip bei der Zinsberechnung und Kreditvergabe, um das Risiko und den erwarteten Ertrag von Finanzprodukten realistisch einzuschätzen.
Weitere Anwendungsbeispiele:
- Berechnung des zukünftigen Hauspreises bei Inflation.
- Bestimmung des Zinssatzes eines Kredits anhand der monatlichen Raten.
- Vergleich zwischen verschiedenen Finanzierungsmodellen (z. B. Barzahlung vs. Ratenzahlung).
- Berechnung der Dauer, bis sich eine Investition verdoppelt (z. B. mit logarithmischer Umstellung).
Beispiel für den Zeitwert des Geldes beim Investieren
Ein Investor muss sich zwischen zwei identischen Projekten entscheiden, die sich nur in der Auszahlung des Cashflows unterscheiden:
- Projekt X zahlt 200.000 EUR bereits nach einem Jahr aus.
- Projekt Y zahlt 200.000 EUR erst nach fünf Jahren aus.
Da Geld über die Zeit an Wert verliert, berechnet er den Barwert (PV) der zukünftigen Zahlungen. Angenommen, der Zinssatz beträgt 5 % pro Jahr, dann ergibt sich:
- Projekt X: Der Barwert der 200.000 EUR nach einem Jahr beträgt 190.476,19 EUR.
- Projekt Y: Da das Geld erst in fünf Jahren ausgezahlt wird, sinkt sein heutiger Wert auf 156.705,23 EUR.
Obwohl beide Projekte den gleichen nominalen Betrag auszahlen, ist Projekt X finanziell attraktiver, da das Geld früher zur Verfügung steht und wieder investiert werden kann.
Kostenloses Webinar + PDF: So handelst du profitabel mit Optionen und generierst ein Zusatzeinkommen
Lerne in unserem kostenlosen Live-Webinar am 28.04.2025 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.